Las cartas mágicas

Reproduzca cada una de las siguientes cartas y podrá adivinar cualquier número entre 1 y 100 que uno de sus amigos haya pensado.




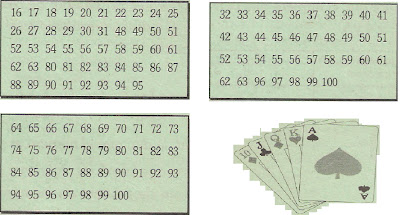
 Vaya enseñando cada una de las cartas a su amigo(a), pidiéndole que solamente indique en cuáles está el número que pensó.

PARA ADIVINAR EL NÚMERO
       Usted debe sumar los números que aparecen en la parte superior izquierda de cada una de las cartas que el indicó; el resultado es el número que su amigo pensó.


Relación del juego con el sistema binario

Todos los números del sistema decimal se pueden escribir en sistema binario, éstos aparecen representados únicamente con unos y ceros.    Para llevar a cabo nuestro juego, tengamos presente que en las cartas que nos digan SÍ, representarán un UNO y las que nos digan NO, representaran un CERO.  

Carta 7
Carta 6
Carta 5
Carta 4
Carta 3
Carta 2
Carta 1
Grupos de
2x2x2x2x2x2
Grupos de
2x2x2x2x2
Grupos de
2x2x2x2
Grupos de
2x2x2
Grupos de
2x2
Grupos de
2
Unidades
64
32
16
8
4
2
1

Ejemplo:

Un amigo pensó en el número 19, por lo tanto al mostrarle las cartas él nos dijo que su número se encontraba en las CARTAS 1, 2 y 5.

Carta 7
Carta 6
Carta 5
Carta 4
Carta 3
Carta 2
Carta 1
no
no
sí
no
no
sí
sí
0
0
1
0
0
1
1
64
32
16
8
4
2
1

Y al escribir éste número en binario quedaría de la siguiente manera


16x 1  +  8x0  +  4x0  +  2x1 + 1x1  --------  10011(2)
 16    +    0     +    0    +    2   +  1      --------19

Que tal si hubieran pensado en el 85...

Carta 7
Carta 6
Carta 5
Carta 4
Carta 3
Carta 2
Carta       1
sí
no
sí
no
sí
no
sí
1
0
1
0
1
0
1
64
32
16
8
4
2
1


 64x1 + 32x0  + 16x1  + 8x0  + 4x1 + 2x0 + 1x1  ----  1010101(2)
  64   +     0     +  16    +    0    +   4    +   0   +  1      --------85

Etiquetas: , , ,

No hay comentarios:

Publicar un comentario

DESAFÍO MENTAL